선형 회귀와 로지스틱 회귀
회귀 분석
회귀 분석(Regression Analysis)은 학창시절 방정식 문제와 유사합니다.
함수 ‘f(x) = y’라고 할 때, x와 y의 관계를 밝히는 것, 다시 말하면 둘 이상의 변수 사이의 함수 관계를 찾는 것입니다.
이때 x는 독립변수(Independent variable) 혹은 설명변수(Explanatory variable)라고 하고, y는 종속변수(Dependent variable) 혹은 반응변수(Response variable)라고 합니다.
정리하면 “독립변수와 종속변수 사이의 상호 관련성을 규명하는 것”이라고 할 수 있습니다.
ex) 아버지 키와 자식의 사이의 관계 연구
선형 회귀
정의
선형 회귀(Linear Regression)이란 변수의 관계를 직선 형태로 가정하고 분석하는 것입니다.
용어
다음은 기본적인 선형 회귀 방정식입니다.
$y=\beta x + \epsilon$
선형 회귀 방정식에서 $\beta$와 $\epsilon$는 회귀 모델로부터 추정하는 파라미터입니다.
- $\beta$ : 회귀 계수
- $\epsilon$ : 종속 변수와 독립 변수 간 오차
머신러닝 모델에서 선형 회귀는 다음과 같이 표현합니다.
$H = Wx + b$
마찬가지로 $H, W, b$는 회귀 모델로부터 추정하는 파라미터입니다.
- $H$ : 가정 (Hypothesis)
- $W$ : 가중치 (Weight)
- $b$ : 편향 (bias)
회귀 분석의 최종적인 목표는 잔차를 최소화하는 파라미터를 구하는 것입니다!
잔차(Residuals) 회귀 모델이 예측한 값과 실제 값의 차이, 즉 오차를 말합니다.
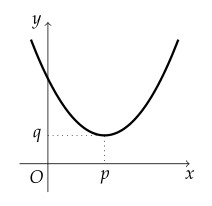
이 2차 함수 그래프가 손실 함수의 그래프이며, 세로축은 오차(loss) 가로축은 파라미터(가중치)라고 가정하겠습니다.
그렇다면 가로축에서 $p$인 점을 알아야 합니다. 위 그래프에서 $p$인 점의 기울기는 0입니다.
따라서 잔차를 최소화하는 파라미터를 구한다는 건 다시 말하면 손실 함수에서 기울기가 0에 가까운 점을 찾아가는 과정입니다.
가중치가 $O$에서 $p$ 방향으로 커진다면 다음과 같은 식으로 가중치를 업데이트할 수 있습니다.
$W := W - a \frac{\partial J(x)}{\partial W}$
$a$는 learning rate입니다.
$O$와 $p$ 사이에서 기울기(미분 계수)는 음수이므로 $O$와 $p$ 사이에서 가중치는 점점 커지고,
$p$ 보다 클 때 기울기(미분 계수)는 양수이므로 $p$ 보다 클 때 가중치는 점점 작아집니다.
이러한 방식으로 최적화 하는 기법을 경사하강법이라고 합니다.
경사하강법 기울기를 구하고 경사의 절댓값이 낮은 쪽으로 이동, 극값에 이를 때까지 반복하는 알고리즘을 말합니다.
기본 가정
적절한 선형 회귀 분석을 위해서는 다음 네가지 조건을 만족해야합니다.
- 선형성 : 독립변수와 종속변수의 관계가 선형적임
- 독립성 : 서로 다른 독립변수 간 상관관계가 없음
- 등분산성 : 독립변수의 변화에 따른 오차의 분산이 일정함
- 정규성 : 오차의 학률 분포가 정규 분포를 따름
로지스틱 회귀
정의
로지스틱 회귀란 데이터가 어떤 범주에 속할 확률을 구하는 것입니다.
이때 확률은 0과 1 사이의 값으로 0에 가까우면 해당 범주에 속하지 않는 것으로, 1에 가까우면 해당 범주에 속하는 것으로 예측합니다.
로지스틱 회귀 분석은 아래와 같은 작업을 수행합니다.
- Odds 구하기
- log-Odds에 Sigmoid 함수를 취하여 0과 1 사이의 확률 구하기
- 일정 이상의 확률을 얻을 경우 분류하기
Odds
오즈(Odds)는 사건이 발생할 확률을 사건이 발생하지 않을 확률로 나눈 값입니다.
간단하게 쓰면 Odds = (사건이 발생할 확률) / (사건이 발생하지 않을 확률) 입니다.
$odds = \frac{P(y=1|x)}{P(y=0|x)} = \frac{P}{1-P}$
다시 말하면 오즈는 사건이 발생할 확률이 사건이 발생하지 않을 확률 대비 얼마나 높은 지에 대한 지표입니다. 로지스틱 회귀 분석에서는 이러한 오즈에 로그를 취한 값을 사용합니다.
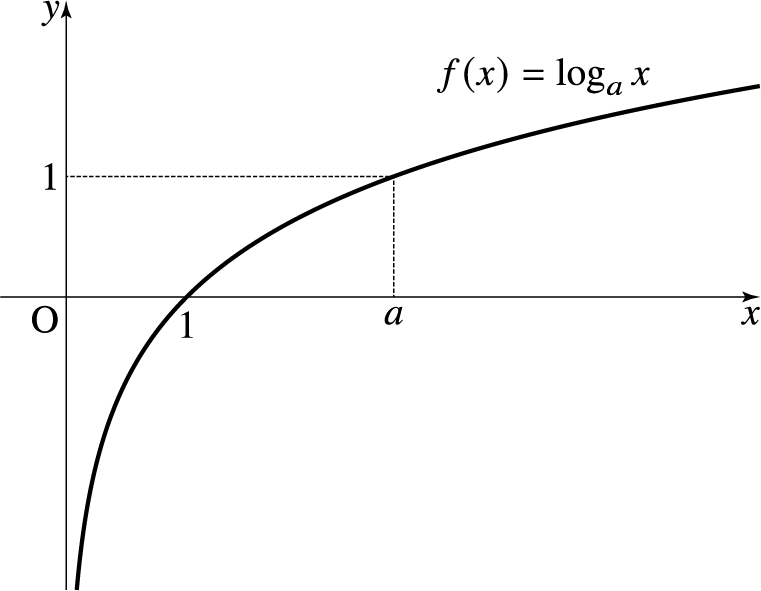
오즈에 로그를 씌운 결과는 다음과 같습니다.
- 사건이 일어날 확률이 사건이 일어나지 않을 확률보다 낮은 경우 (Odds < 1) → 음수
- 사건이 일어날 확률이 사건이 일어나지 않을 확률보다 높은 경우 (Odds > 1) → 양수
- 사건이 일어날 확률과 사건이 일어나지 않을 확률이 같은 경우 (Odds = 1) → 0
- 사건이 일어날 확률이 사건이 일어나지 않을 확률에 비해 현저하게 낮은 경우 (Odds = 0) → 음의 무한대
- 사건이 일어날 확률이 사건이 일어나지 않을 확률에 비해 현저하게 높은 경우 (Odds = $\infty$) → 양의 무한대
오즈에 로그를 씌우면 값의 범위가 음의 무한대에서 양의 무한대까지 확장되어 회귀 분석이 가능하게 됩니다.
오즈에 로그를 씌운 값 log-odds를 로짓(logits)이라고 합니다.
Sigmoid
로지스틱 회귀에서 활성화 함수로 시그모이드 함수를 이용할 수 있습니다.
시그모이드 함수는 0과 1 사이의 값으로 매끄럽게 반환합니다.
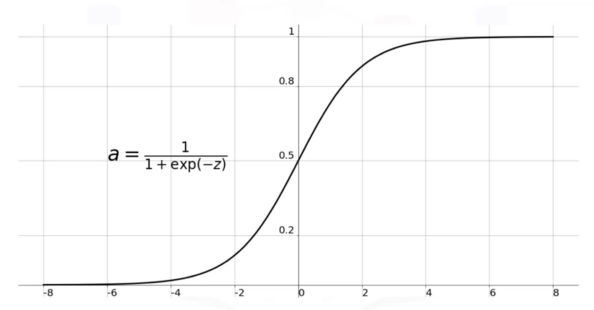
시그모이드를 통해 얻은 확률이 사전에 정의한 임계치(threshold) 이상일 경우 분류를 수행합니다.
다시 정리하면 로지스틱 회귀 분석은 다음과 같은 작업을 수행합니다.
- Odds 구하기
- log-Odds에 Sigmoid 함수를 취하여 0과 1 사이의 확률 구하기
- 일정 이상의 확률을 얻을 경우 분류하기
다중 로지스틱 회귀
위에서 소개한 로지스틱 회귀는 양성/음성, 성공/실패 등 이진 분류에만 적용 가능합니다.
종속변수(분류하고자 하는 범주)가 2개 이상인 경우 다중 로지스틱 회귀를 사용합니다.
다중 로지스틱 회귀에서 활성화 함수는 softmax 함수를 사용합니다.
$softmax (x) = e^{x_i}/\sum e^{x_j}$
softmax도 마찬가지로 0과 1 사이의 확률을 반환합니다.
softmax의 특징은 함수 값의 총합이 1이라는 것입니다.
따라서, 한 샘플 데이터의 각각 클래스에 대한 확률을 구하여 분류를 수행할 수 있습니다.