L1과 L2 Regularization
개념
Regularization은 한국어로 정규화로 불립니다.
흔히 정규화라고 불리는 것은 Regularization 말고도 Normalization이 있습니다.
머신러닝에서 Regularizaiton과 Normalization은 모두 모델의 과적합을 방지하기 위해 쓰입니다.
하지만 엄밀히 말하면 Regularization과 Normalizaiton은 다릅니다.
따라서 Regularizaiton을 더 정확한 표현인 정칙화로 부르겠습니다.
정칙화(Regularization)과 정규화(Normalization)는 모두 모델의 과적합을 방지하는 방법입니다.
모델의 과적합이란 모델이 훈련 데이터에만 지나치게 치중되어 새로운 데이터를 적절하게 예측하지 못하는 현상입니다.

초록색 점이 훈련 데이터일 때, 모델은 Optimal case처럼 데이터의 일반적인 분포를 추정해야합니다.
만약 Overfit case라면 훈련 데이터와 완벽히 동일한 데이터가 아니라면 적절히 반응하지 못할 것입니다.
Regularization
정칙화(Regularization)란 임의로 모델의 복잡도를 줄이는 방법입니다.
단순하게 loss가 작아지는 방향으로 학습을 지속한다면 특정 가중치가 큰 값을 가지게 됩니다.
정칙화는 가중치(Weight)가 커지지 않도록 하는 방법입니다.
간단히 말하면 이렇습니다.
정칙화(Regularization) = 모델의 복잡도 ↓ = 모델의 가중치(Weight) ↓
정칙화의 대표적인 예시는 L1 Regularizaiton, L2 Regularization입니다.
Normalization
정규화(Normalization)란 데이터의 형태를 트레이닝에 적합하게 변형하는 방법입니다.
데이터의 분포 특성에 의해 데이터의 거리 간의 측정이 왜곡되는 경우가 있습니다.
예를 들면 아주 큰 범위의 값을 가지고 있는 데이터의 경우 머신러닝에 큰 어려움을 겪을 수 있습니다.
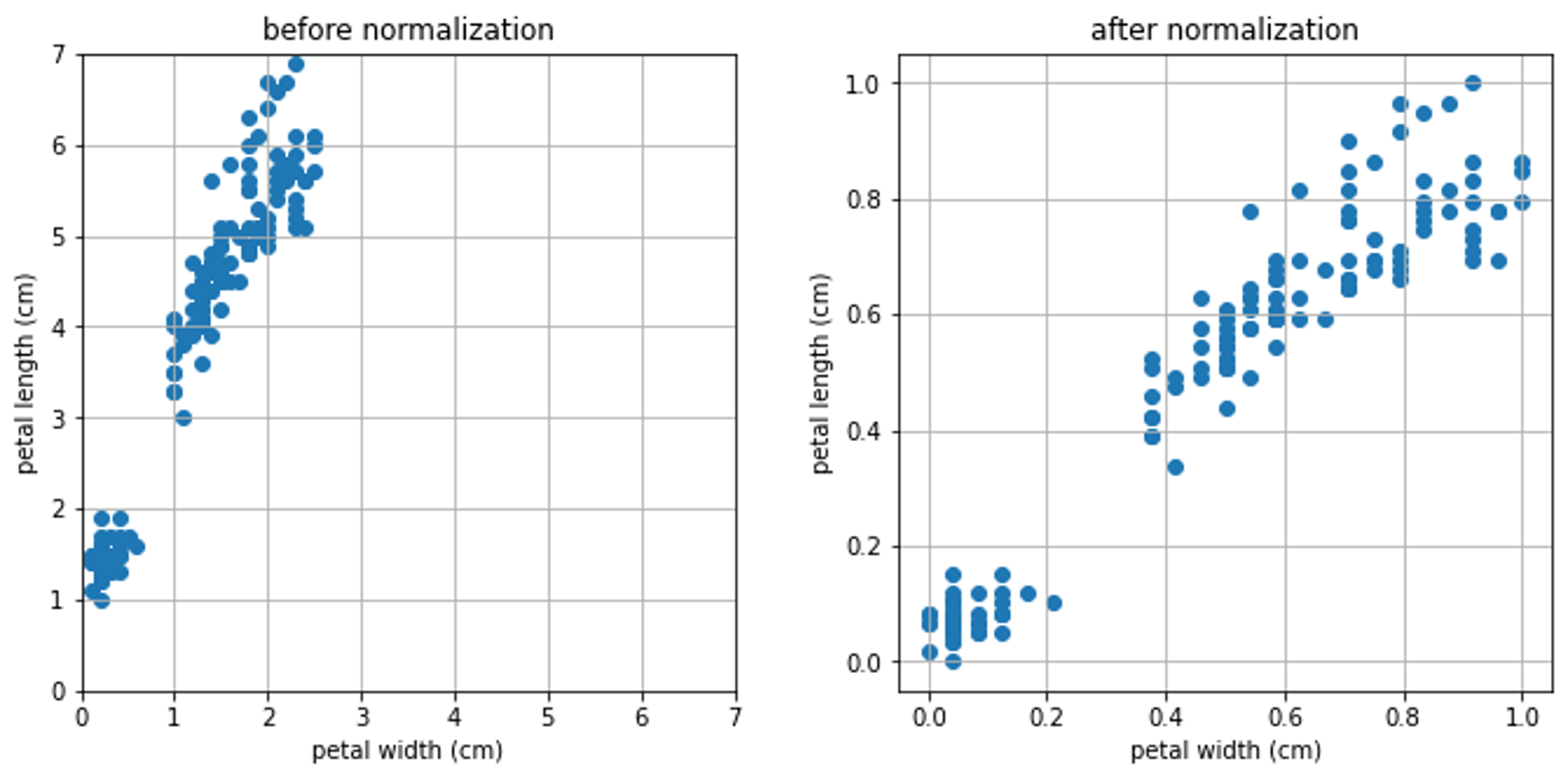
위 이미지는 scikit learn의 iris data입니다.
왼쪽은 정규화를 하지 않은 원본 데이터이고, 오른쪽은 minmax 정규화를 적용한 데이터입니다.
우리는 petal(꽃잎)의 세로 길이와 가로 길이가 동일한 중요도를 가지기를 기대합니다.
하지만 꽃잎의 세로 길이는 대략 1부터 7까지 넓게 퍼져있고 꽃잎의 가로 길이는 대략 0부터 2.5까지 좁게 퍼져있기 때문에,
기계는 본의아니게 꽃잎의 세로 길이에 더 큰 중요도를 두게 됩니다.
정규화의 대표적인 예시는 z-score, minmax scaler입니다.
z-score 통계학적 정규분포를 만들고, 표준편차 위 어디에 위치하는지 표현하는 지표입니다.
minmax 각각의 값들을 0과 1 사이의 값으로 변환하는 방법입니다.
L1 Regularization
L1 Regularization의 정의는 다음과 같습니다.
$\hat{\beta}^{lasso} := argmin_{\beta} \frac{1}{2n}$$\sum_{i=1}^{n} (y_i - \beta_0 - \sum_{j=1}^{p} x_{ij}\beta_j)^2$ $+$$\lambda \sum_{j=1}^{p} \vert \beta_j \vert$
요약하면 loss와 lambda X norm의 합으로 볼 수 있습니다.
($p$는 $x$의 차원 수)
Loss
L1 Regularization에서 loss 부분은 다음과 같습니다.
$\sum^{n}_{i=1}(y_i - \beta_0 - \sum^{p}_{j=1}x_{ij}\beta_j)^2$
원래 L1 loss이자 MAE(Mean Absolute Error)의 정의는 다음과 같습니다.
$\frac{1}{n}\sum^{n}_{i=1} \vert y_i - f(x_i) \vert$
비교해보면 prediction을 $\sum^{n}_{i=1} f(x) = x\beta$로, target을 $y$로 해석할 수 있겠습니다. 그렇다면, $\beta_0$는 절편입니다.
L1 Regularization에서 L1 loss를 사용하지 않는 이유는 L1 loss의 형태가 경사하강법을 적용하기 어렵기 때문입니다.
따라서, L2 loss이자 MSE(Mean Squared Error)인 위 식을 사용합니다.
경사하강법 미분을 통해 기울기를 구하고 경사의 절댓값이 낮은 쪽으로 이동, 극값에 이를 때까지 반복하는 알고리즘을 말합니다.
norm
L1 Regularization에서 lambda X norm 부분은 다음과 같습니다.
$\lambda \sum_{j=1}^{p} \vert \beta_j \vert$
lambda는 임의의 값으로 0에 가까울수록 정규화의 효과가 적고, 클수록 정규화의 정도가 큽니다.
다시 말하면 lambda는 가중치가 작은 벡터를 0에 가깝게 합니다.
norm이란 벡터의 크기 혹은 벡터의 거리를 구하는 공식입니다.
L1 norm의 정의는 다음과 같습니다.
$\vert\vert x \vert\vert := \sum^{n}_{i=1}\vert x_i \vert$
L2 Regularization
L2 Regularization의 정의는 다음과 같습니다.
$\hat{\beta}^{ridge} := argmin_{\beta} \frac{1}{2n}$$\sum_{i=1}^{n} (y_i - \beta_0 - \sum_{j=1}^{p} x_{ij}\beta_j)^2$ $+$$\lambda \sum_{j=1}^{p} \vert \beta_j^2 \vert$
마찬가지로 loss와 lambda X norm의 합으로 볼 수 있습니다.
($p$는 $x$의 차원 수)
Loss
L2 Regularization에서 loss 부분은 L1 Regularization과 동일합니다.
$\sum^{n}_{i=1}(y_i - \beta_0 - \sum^{p}_{j=1}x_{ij}\beta_j)^2$
위 식은 L2 loss이자 MSE(Mean Squared Error)을 따릅니다.
$\frac{1}{n}\sum^{n}_{i=1} (y_i - f(x_i))^2 \vert$
norm
L2 Regularization에서 lambda X norm 부분은 다음과 같습니다.
$\lambda \sum_{j=1}^{p} \vert \beta_j^2 \vert$
L2 norm의 정의는 다음과 같습니다.
$\vert\vert x \vert\vert := \sum^{n}_{i=1} x_i^2$